| Pr(X=x|n,p) = n!/[x! (n-x)!] . px .
(1-p)n-x |
|
Most of the experiments I described previously had large sample sizes (viz the first table). Therefore, there is little difficulty accepting the fact that the segregation ratios are actually 1:3 or 1:1:1:1, and variations from the exact ratio are due to chance. To interpret results from smaller samples, such as those seen in human families, requires knowledge of probability and statistics.
The frequentists (a sect of statisticians) would say there are a (potentially) infinite number of offspring of our experimental cross, of which we are getting to see only a finite subset or sample. The sample space S of outcomes for a single experiment (one child) is A (with genotype A/A or A/a) or a (a/a) - two mutually exclusive events. If we count N offspring, of which NA express the A phenotype, then the probability of A is,
From this one can see that,
1 >= Pr(A) >= 0
Pr(S) = Pr(A or a) = 1
Pr(Not A) = Pr(a) = 1 - Pr(A).
For this experiment, Pr(A)= 3/4, Pr(a)= 1/4.
If we repeat the experiment, the result for the second child is independent of that for the first child. The probabilities for the joint events are obtained by multiplying the probabilities for each contributing event.
| One Child | Two Children | Three Children |
| A 3/4 | A,A 9/16 | A,A,A 27/64 |
| a 1/4 | A,a 3/16 | A,A,a 9/64 |
| a,A 3/16 | A,a,A 9/64 | |
| a,a 1/16 | A,a,a 3/64 | |
| a,A,A 9/64 | ||
| a,A,a 3/64 | ||
| a,a,A 3/64 | ||
| a,a,a 1/64 |
In the case of segregation ratios, where we are only interested in the total counts, the order in which the offspring were born is irrelevant. This count (X, say) is a random variable, which for a sibship of three children can take four values according to a particular probability distribution function (Pr(NA=X)):
| X | Pr(NA=X) | Pr(NA<=X) |
|---|---|---|
| 3 | 27/64 | 64/64 |
| 2 | 27/64 | 54/64 |
| 1 | 9/64 | 27/64 |
| 0 | 1/64 | 1/64 |
X in this case is comes from the binomial distribution with parameters n=3 and p=3/4. If we observed a large number of samples of size 3, with Pr(A)=3/4, the average or expectation for X would approach,
as our earlier definition of probability would lead us to expect.
We can use this understanding in a number of ways. Say we are given only three progeny arising from an F2 cross (P1: A a), and observe zero out of three were A. Is it likely that A or a is the dominant phenotype? From the tabulation, we can see that if A is dominant over a, the probability of observing such an outcome is only 1/64. If the converse was true, the probability of such an outcome would be 27/64.
We will define one possibility A > a as the null hypothesis (the base hypothesis or H0) and a > A the alternative hypothesis (H1). The likelihood ratio for testing these two alternatives (in this simple case) is 27/64 divided by 1/64, which is 27. This says that a being dominant over A is 27 times more likely than the null hypothesis. In linkage analysis, we normally take the decimal log of this ratio (the LOD score), which in this case is 1.43.
It is necessary then to choose a size of likelihood ratio that we regard as "conclusive proof" that one hypothesis is correct, and the other incorrect. In linkage analysis, a ratio of 1000 (LOD=3) is the number that has been chosen, at least partly, arbitrarily.
The alternative viewpoint is to perform a one-sided test (in the direction of H1) of the null alone. If the null hypothesis (A>a) was true, we would see the observed result only in 1/64 replications (on average). This is the so-called Type I error rate. Traditionally, we set a critical P-value (probability of a result at least as extreme as the one observed) of 1/20. Using this criterion (alpha=0.05), we would reject H0, and accept H1.
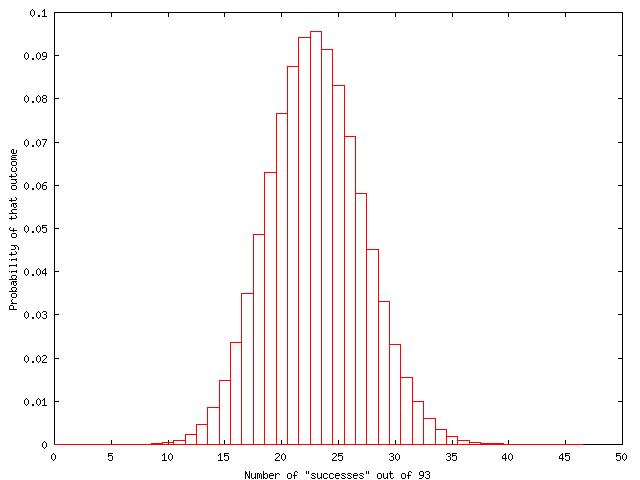
If we did not have a specific hypothesis (such as dominance), we might be inclined just to estimate Pr(A), and perhaps give a measure of how accurate this estimate is. We can do the latter by replacing the p parameter in the binomial probability function with an estimate from the sample. The sample size in the last example is too small for this, so I'll return to the frizzling cross where 23/93 chickens in the F2 were frizzled.
We set p=23/93. Then the probabilities of each possible count out of 93 can be calculated
| Pr(X=x|n,p) = n!/[x! (n-x)!] . px .
(1-p)n-x |

|
The central 95% confidence interval is constructed by systematically adding up the probabilities on either side of the point estimate for p to give upper and lower values of X that contain 0.95 of the probability (so 0.475 on either side). So the estimate for the segregation ratio is 24.7% with 95% confidence interval from 16.4% to 34.8%. We might say that we are fairly (95%) certain that the segregation ratio is between 4/25 and 1/3, and because of the bell shape of the distribution, most likely to be close to 1/4.
What determines the width of the confidence interval? The larger the sample size, the narrower the interval. That is, the more precise you can believe your point estimate to be.
Ways to extend the binomial to more than two categories are via the multinomial or Poisson distributions. For example, in the codominant case F2, we can discriminate three categories of outcome: A=A/A, B=A/a, C=a/a; Pr(A)=Pr(C)=1/4; Pr(B)=1/2. For a sample of size N, N=NA+NB+NC, we expect
E(NA)=Pr(A).N; E(NB)=Pr(B).N; E(NC)=Pr(C).N.
Rather than tabulating the exact probabilities (which is a big job), we usually use tests based on asymptotic or large sample theory. Pearson showed in 1900, if NA, NB, NC are large enough, that under the null hypothesis (Pr(A),Pr(B),Pr(C)),
| Phenotype (genotype) | Observed | Expected |
| Frizzled (FF) | 23 | 23.25 (93/4) |
| Sl. Frizzled (Ff) | 50 | 46.50 (93/2) |
| Normal (ff) | 20 | 23.25 (93/4) |
Q = (23-23.25)2/23.25 + (50-46.5)2/46.5 + (20-23.25)2/23.25 = 0.72.
If the null hypothesis was a perfect fit for the observed data, then Q would be 0. If there is any deviation from the null, Q will be greater than zero. In fact, under the null hypothesis, on average Q will be v, E(Q)=2 in this example. The degrees of freedom v is two because of the linear constraint that the probabilities must add up to one. Therefore, if we specify Pr(A) and Pr(B) for our null hypothesis, Pr(C) is not free to be anything other than 1-Pr(A)-Pr(B). We can conclude that the data is consistent with the null hypothesis, Pr(Q<=0.72 | v=2)=0.70.
We can also construct a likelihood ratio which compares the null hypothesis to the alternative hypothesis which is specified by the observed counts (Pr(A)=23/94; Pr(B)=50/93; Pr(C)=20/93). This is different from the earlier example where we specified the alternative hypothesis. It turns out that, asymptotically, negative two times the natural log of this likelihood ratio is also distributed as a X2 with two degrees of freedom. Under the assumption of a Poisson (or a multinomial) distribution giving rise to each count, this likelihood ratio X2 (perhaps due to Fisher 1950) is
In the example,
G2 = 2( 23.log(23.5/23) + 50.log(46.5/50) + 20.log(23.5/20)) = 0.31.
The likelihood ratio comparing the observed counts to those expected under Mendelism is approximately 0.86 (close to 1). Finally, we could construct confidence intervals for all three observed probabilities, much in the way we did for one of the probabilities earlier.
We have previously seen this table for a testcross.
| White | Coloured | ||
| Frizzled | 18 | 63 | 81 |
| Normal | 63 | 13 | 76 |
| 81 | 76 | 157 |
The goodness-of-fit tests discussed allow us to determine whether it is plausible that these two loci are in fact unlinked. The null hypothesis has all four cells equal (expected value under this hypothesis 157/4). The Pearson X2 test gives,
(18-39.25)2/39.25+(63-39.25)2/39.25+(63-39.25)2/39.25+(13-39.25) 2/39.25 = 57.8.
and the likelihood ratio X2= 62.5.
These X2's have three degrees of freedom, again because the fourth probability is fixed once the first three are set. This hypothesis actually has three parts (one for each degree of freedom): White and Coloured segregate equally, Frizzled and Normal segregate equally, and White and Frizzled are unlinked.
In the case of the likelihood X2, this is the sum of the three one degree of freedom X2 testing each hypothesis. Pearson X2's cannot be partitioned this way.
| Hypothesis | X2 | d.f. | P-value |
| Pr(White)=Pr(Coloured)=1/2 | 0.16 | 1 | 0.689 |
| Pr(Frizzled)=Pr(Normal)=1/2 | 0.16 | 1 | 0.689 |
| Pr(White & Frizzled)=1/4 | 62.13 | 1 | 3.2210-15 |
| Combined hypothesis | 62.45 | 3 | 1.7610-13 |
This confirms our original qualitative assessment of this table. The 95% confidence interval for the estimate of c=31/157=19.7% is 13.8% to 25.8%.
Linkage leads to deviation from the 9:3:3:1 ratios in the dihybrid intercross (dominant traits), so a test for linkage can be easily constructed. Estimating c is more complex, because we have to determine whether each parent's genotype was in coupling or repulsion. For example, the proportion of double recessive offspring under no linkage this is 1/16. If the mating is Coupling Coupling (AB/ab AB/ab), then this proportion is (1-c)2/4; if it was Repulsion Repulsion (Ab/aB Ab/aB), c2/4.
In the Frizzled test-cross data, there were two crosses, one in coupling, and the other in repulsion. These seemed to give similar estimates for the recombination fraction between the two loci, but it would be useful to have a test for equality of homogeneity of these estimates.
Our null hypothesis is then c1=c2. The observed counts were:
| Recombinant | Non-recombinant | |
| Cross 1 | 31 (19.7%) | 126 |
| Cross 2 | 6 (18.2%) | 27 |
If the null hypothesis is true, then both strata have the same expectation, and the best estimate for c will be (31+6)/(157+33)=19.47%. We can use this pooled estimate as the expected values for a X2 test:
| Recombinant | Non-recombinant | |
| Cross 1 | 30.6 (19.5%) | 126.4 |
| Cross 2 | 6.4 (19.5%) | 26.6 |
This gives a one degree of freedom X2=0.04, because there are two original proportions being explained by one hypothetical proportion. If there were six crosses, then there would be five degrees of freedom. This test is also known as the 2xN Pearson contingency chi-square.
I have been using the Poisson distribution without having described it. If we return to a series of experiments described by the binomial distribution where the (constant) probability of a success Pr(A) or p is very small, but the number of experiments N or n is large so that the expected value of NA (np) is "appreciable", then the probability distribution function will approach,
where m is E(NA).
This distribution is very attractive. Unlike the binomial, where X is limited to be between zero and N, the Poisson hasn't specified the number of experiments, just that is greater than zero. Given the derivation, one can see why the Poisson distribution can be used to estimate the binomial probabilities when p is small. Furthermore, for multinomial data, we can regard each cell of counts as coming from a separate Poisson distribution of a given mean (mi), given by NPr(i).
Other uses for the Poisson arise when we obtain counts arising from a period of time or a subdivision of length or area. The number of offspring during the lifetime of a mating is often modelled as being Poisson. Similarly, it has been used to describe the number of recombination events along the length of a chromosome (it underlies the choice of the Haldane mapping function).
We have examined one limiting distribution for the binomial, the Poisson. If we increase the n parameter (regardless of p), then the binomial probability distribution function approaches the Gaussian or Normal distribution. The same is true for the X2 distribution when v becomes large, and the Poisson distribution when m is large.
The Gaussian has a continuous, symmetrical, bell shaped probability distribution. It has two defining parameters, mu and sigma, which conveniently are the mean and standard deviation. The approximations then to various distributions then given using:
| mu | sigma2 | |
|---|---|---|
| Binomial | np | np(1-p) |
| Poisson | m | m |
| Chi-square | v | 2v |
These and other equalities allow a number of asymptotic tests to be constructed.
Fisher and Snell (1948) report results from mice testcrossed for two traits jerker and ruby.
| Group | + + | je | ru | ruje |
|---|---|---|---|---|
| Cambridge (female, coupling) | 51 | 48 | 30 | 44 |
| Bar Harbour (female, coupling) | 32 | 30 | 31 | 47 |
| Cambridge (male, coupling) | 17 | 12 | 15 | 17 |
| Bar Harbour (male, coupling) | 20 | 13 | 13 | 14 |
| Cambridge (female, repulsion) | 4 | 4 | 6 | 4 |
| Cambridge (male, repulsion) | 5 | 5 | 4 | 8 |
Are je and ru linked? What statistical test would you perform? What result does it give? Would any single one of these studies be enough to decide without the others?