David L. Duffy, MBBS PhD.
QIMR Berghofer Medical Research Institute,
300 Herston Road,
Herston, Queensland 4029, Australia.
Email: davidD@qimr.edu.au
Version 1: 2009-01-10
I have included three genome-wide SNP datasets here, so you can get a feel for handling large amounts of data. You will soon realize that you need as much memory as possible on your computer, and that some programs that are perfectly fine for linkage size datasets are too slow with these large files.
Amyotrophic Lateral Sclerosis is a degenerative disease of motor neurons that occurs in familial (10%) and "sporadic" forms. The incidence is 2-3/100000 per annum. A number of high penetrance loci have been identified for familial cases:
SOD1 (20% of familial cases), NEFH, PRPH, SETX, APB, ANG, TARDBP, DCTN1.
A recent paper has suggested variation around ELP3 may be associated, while GWAS studies also implicate ITPR2 and DPP6 (best SNP rs10260404). Cronin et al (2009) found the latter association did not replicate in additional Polish and Irish case samples.
One sensible strategy would be to test SNPs near these genes for association to ALS.
This dataset is a PLINK version of the HapMap 1-2 data for Japanese and (Han) Chinese samples. The trait in this example is ethnicity. These two populations are quite close genetically, but with the large number of SNPs available, it is easy to separate the two populations.
This dataset was one of the first GWAS datasets made available to the general scientific community. There are ``sister'' GWAS of ALS that are also available for download, see the dbGaP website. These can be combined with the present data and jointly analysed, or the P-values or summary statistics can be combined in a metaanalysis.
The dataset was produced by the Laboratory of Neurogenetics, of the intramural program of the National Institute on Aging, National Institutes of Health. The genotyping was performed using the Illumina Infinium assays; HumanHap240S, HumanHap300-Duo and HumanHap500. These Infinium assays assess haplotype tagging SNPs based upon Phase I+II of the International HapMap Project. The control genotype data consists of 555,352 SNPs from 271 neurologically normal individuals and 276 Amyotrophic lateral sclerosis patients
Reference: Schymick J, Scholz SW, Fung HC, Britton A, Arepelli S,
Gibbs JR, Lombardi F, Matarin M, Kasperaviciute D, Hernandez DG, Crews
C, Bruijn L, Rothstein J, Mora G, Restagno G, Chiò A, Singleton A,
Hardy J, Traynor BJ. Genome-wide genotyping in amyotrophic lateral
sclerosis and neurologically normal controls. Lancet Neurol. in press.
Fung HC, Scholz S, Matarin M, Simon-Sanchez J, Hernandez D, Britton A,
Gibbs JR, Langefeld C, Stiegert ML, Schymick J, Okun MS, Mandel RJ,
Fernandez HH, Foote KD, Rodriguez RL, Peckham E, De Vrieze FW,
Gwinn-Hardy K, Hardy JA, Singleton A. Genome-wide genotyping in
Parkinson's disease and neurologically normal controls: first stage
analysis and public release of data. Lancet Neurol. 2006
Nov;5(11):911-6.
Source: https://queue.coriell.org/q/
This is data from the draft release 1.0 for the third phase of the HapMap project (HapMap III). Data consist of:
(i) SNP genotype data generated from HapMap Phase III samples (including the original HapMap samples used in Phase I and II of the International HapMap Project). In total, this release contains genotypes data from 1115 individuals from 11 populations, collected using two platforms: the Illumina Human1M (WTSI) and the Affymetrix SNP 6.0 (BI). Data from the two platforms have been merged for this release.
The populations are:
Genotyping concordance between the two platforms was 0.9931 (computed over 249889 overlapping SNPs). The data was merged using PLINK (--merge-mode 1), keeping only genotype calls if there is consensus between non-missing genotype calls (that is, merged genotype is set to missing if the two platforms give different, non-missing calls).
Quality control at the individual level was performed separately for different platforms. Only individuals with QC passed genotype data on both platforms were kept in this release. The following criteria were used to keep SNPs in the data sets of this release:
The "consensus" data set contains data for all individuals (558 males, 557 females; 924 founders and 191 non-founders), only keeping SNPs that passed QC in all populations (overall call rate is 0.998). The "consensus/polymorphic" data set has In all genotype files, alleles are expressed as being on the (+/fwd) strand of NCBI build 36.
Again, we can treat ethnic group as the phenotype of interest, and test for differences.
We'll first look at an example of why data cleaning is important for GWAS data. We'll analyse some data before cleaning. Here are results for the best five SNP association results from chromosome 1 in the ALS dataset without cleaning. These were obtained using my Sib-pair program using this script: chr1.in.
>> sum
Total number of tests = 41573
Locus Position P-value -log10(P)
-------------- ---------- ------- ----------
rs2473323 22.26 0.0000 8.505 22261913 (chr 1) A>C 0.089 failed=25
rs2363451 198.13 0.0000 6.210 198130177 (chr 1) A>G 0.012 failed=23
rs2336938 204.69 0.0000 4.549 204685421 (chr 1) A>C 0.457 failed=0
rs10493702 82.02 0.0000 4.502 82017730 (chr 1) C>T 0.022 failed=51
rs1288331 53.40 0.0000 4.463 53403636 (chr 1) A>G 0.333 failed=0
>> tab trait rs2363451
------------------------------------------------
Cross-tabulation of "trait" ... "rs2363451"
------------------------------------------------
rs2363451
trait A/A A/G G/G Allele Freq Exact HWE-P
-----------------------------------------------------------------
n 233 (.860) 35 (.129) 3 (.011) 0.9244 0.0756 0.1843
y 247 (.976) 6 (.024) 0 (.000) 0.9881 0.0119 1.0000
-----------------------------------------------------------------
Total 480 [.916] 41 [.078] 3 [.006]
No. complete observations = 524
LR contingency chi-square = 26.65
Degrees of freedom = 2
Asymptotic P-value = 0.0000
Empiric P-value = 0.0000 (5240000 MCMC iterations)
Trend chi-square = 22.83 (P=0.0000)
Note the last column of the summary data "failed=25", "failed=23" and "failed=53". Should we expect 3 out of the best 5 association results to have so many failures?
> x <- read.table("cc555k_chr1.snps")
> x2 <- read.table("usals555k_chr1.snps")
> head(x)
> names(x2) <- names(x) <- c("chr", "pos", "SNP", "A1", "A2", "P1", "P2", "failures")
> failures <- x$failures + x2$failures
> table(failures)
> ?ecdf
> plot(ecdf(failures), ylim=c(0.85, 1))
> cumsum(table(failures))/41573
> 1-cumsum(table(x$failures))[1:23]/41573
0.40004330 0.23176100 0.16580473 0.12806389 0.10379333 0.08681115 0.07372574
7 8 9 10 11 12 13
0.06381546 0.05597383 0.04974382 0.04493301 0.04041084 0.03624949 0.03300219
14 15 16 17 18 19 20
0.03009165 0.02766218 0.02544921 0.02318813 0.02160056 0.01979650 0.01830515
21 22
0.01691001 0.01602001
What are these probabilities?
> p <- dbinom(0:5,5,0.016)
> names(p) <- 0:5
> p
0 1 2 3 4 5
9.225194e-01 7.500157e-02 2.439076e-03 3.965977e-05 3.224371e-07 1.048576e-09
> format(p, scientific=F)
> cat(format(p, scientific=FALSE),
labels=paste("Pr(",as.character(0:5)," out of 5)",sep=""),fill=1)
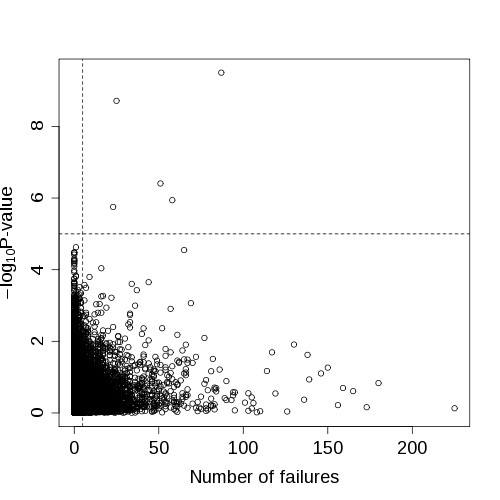
This has all been a bit "rough and ready", but it suggests that SNPs with more genotyping problems tend to give more significant association P-values.
| Chromosome 1 ALS association P-values versus number of assay failures (drawn using failureplot.R) |

|
Is there an obvious reason why?
| A/A | A/G | G/G | Minor Allele Frequency | FAILURES | |
|---|---|---|---|---|---|
| Unaffected | 233 (.860) | 35 (.129) | 3 (.011) | 0.0756 | 0 |
| Affected | 247 (.976) | 6 (.024) | 0 (.000) | 0.0119 | 23 |
> t1 <- table(cut(x$failures,c(-1, 0,5,20,200)), cut(x2$failures,c(-1, 0,5,20,200))) > t1 > chisq.test(t1)
| Failures among Cases | |||||
|---|---|---|---|---|---|
| 0 | 1-5 | 6-20 | 21- | ||
| Failures Among Controls | 0 | 24942 | 5159 | 295 | 22 |
| 1-5 | 4840 | 3920 | 672 | 46 | |
| 6-20 | 78 | 586 | 702 | 57 | |
| 21- | 1 | 7 | 106 | 140 | |
The table above is actually the same setup as a transmission-disequilibrium test. Can you see why I say this?
Earlier, I mentioned some criteria we use to clean GWAS (or indeed genetic) data:
The last criterion is based on the fact that if a genotype is rare, it only takes a few errors in genotyping to lead to a significant change in frequencies. The downside is that we may miss some significant associations, but unless our study is large, usually we won't have enough power anyway.
Choice of an actual threshold for any one of these tests is a little arbitrary. We could perform a detailed analysis of the different error types, but usually we use conservative cutoffs:
| Criterion | PLINK option | Threshold(s) |
|---|---|---|
| Dropout by individual | --mind | 0.1 |
| Dropout by SNP | --geno | 0.1 |
| Minimum allele frequency | --maf | 0.01 |
| Mendelian errors (ped,SNP) | --me | 0.1 0.1 |
| Hardy-Weinberg Disequilibrium | --hwe | 0.001 |
For example, the ALS chromosome 1 SNP dropout criterion is 54 failures. But we will carry out the actual cleaning on the entire dataset, so we have maximum information about individuals.
First we need to combine all the map files and all the pedigree files together. A convenient way to do this is using PLINK's "--merge-list" option.
The merge-list file contains the list of all the files we wish to merge together. We will need to create PLINK style map files, since the ALS files are a different format. Fortunately, they do contain all the information we need for PLINK:
| chromosome (1-22, X, Y or 0 if unplaced) |
| rs# or snp identifier |
| Genetic distance (morgans) |
| Base-pair position (bp units) |
I will create the files using R
# read in the ".snps" file
map <- read.table("cc555k_chr12.snps")
# keep columns 1, 3, 2 (and repeat column 2)
newmap <- map[, c(1,3,2,2)]
# the third column of the map file is supposed to be Morgans
# which we'll fill in with Mbp
newmap[, 3] <- newmap[,3]/1000000
#
# And write out the new file,
# WITHOUT row names, column names, or quotation marks
write.table(newmap, "cc555k_chr12.map",
quote=F,
row.names=F,
col.names=F)
To avoid rewriting this 48 times, I will write a loop:
for (group in c("usals555k_chr", "cc555k_chr")) {
for (chrom in c(as.character(1:23),"X","Y","XY")) {
ifil <- paste(group, chrom, ".snps", sep="")
ofil <- paste(group, chrom, ".map", sep="")
map <- read.table(ifil)
newmap <- map[, c(1,3,2,2)]
newmap[, 3] <- newmap[,3]/1000000
write.table(newmap, ofil, quote=F, row.names=F, col.names=F)
}
}
This should automatically convert the files to the correct format. Then we can run:
plink --file als_all1 --merge-list rest.txt --make-bed --out als1
where rest.txt contains:
usals555k_chr2.map usals555k_chr2.pre cc555k_chr2.map cc555k_chr2.pre usals555k_chr3.map usals555k_chr3.pre cc555k_chr3.map cc555k_chr3.pre [...]
Given that the phenotypes in this dataset are simple, the actual analysis is quite straightforward, whichever package we use.
In Plink (we will use the example problem as a template):
plink --file als_all --make-bed --out als1
plink --bfile als1 --out validate
plink --bfile als1 --maf 0.01 --geno 0.05 --mind 0.05 \
--hwe 1e-3 --make-bed --out als_clean
plink --bfile als_clean --assoc --out als_res
As I noted earlier, there are a number of regions previously associated with ALS risk. For SNPs within these regions, it is reasonable to use a less strict critical P-value, since we have a strong prior hypothesis. In the case of a single SNP association that we wish to replicate, it is usually argued that this is a "preplanned test", so that no Bonferroni correction needs to be made.
An alternative way to think about this is the Bayesian perspective, where we explicitly include an estimate of the prior probability of the truth of a particular hypothesis. In the case of a replication study, the prior odds of the SNP being associated are fairly high, so the test results do not have to be particularly strong. In the case of a SNP taken at random from a GWAS, the prior probability that that SNP is associated is much smaller, say 10000:1 against (Thomas and Clayton 2004).
The conditional error probability is one estimate (actually a lower bound) of the posterior probability that the null hypothesis is true (eg Wakefield 2008):
CEP = 1/(1+ prior/(1-prior) . 1/(-2.718 p log(p)))
p is the P-value for the SNP, and prior is your estimate of the prior probability that the SNP is associated.
| Prior | P-value | CEP |
|---|---|---|
| 0.0001 | 0.0001 | 96% chance null is true |
| 0.01 | 0.0001 | 19% chance null is true |
| 0.1 | 0.0001 | 2% chance null is true |
Unfortunately, we can't put a precise number on the prior probabilities, but we do have a rough idea.
To keep the analysis manageable, I have selected just four of the HapMap3 populations for analysis. To put this file together, I carried out
plink --map hapmap3_r2_b36_fwd.CEU.qc.poly.map \
--ped hapmap3_r2_b36_fwd.CEU.qc.poly.ped \
--make-bed --out ceu
plink --map hapmap3_r2_b36_fwd.TSI.qc.poly.map \
--ped hapmap3_r2_b36_fwd.TSI.qc.poly.ped \
--make-bed --out tsi
plink --map hapmap3_r2_b36_fwd.MEX.qc.poly.map \
--ped hapmap3_r2_b36_fwd.MEX.qc.poly.ped \
--make-bed --out mex
plink --map hapmap3_r2_b36_fwd.ASW.qc.poly.map \
--ped hapmap3_r2_b36_fwd.ASW.qc.poly.ped \
--make-bed --out asw
echo tsi.bed tsi.bim tsi.fam > merge-list.txt
echo mex.bed mex.bim mex.fam >>; merge-list.txt
echo asw.bed asw.bim asw.fam >>; merge-list.txt
plink --bfile ceu --merge-list merge-list.txt \
--make-bed --out fourpops
The merge is the slowest part of this procedure, and can take over an hour, so David J. has already done the merge for us!
For the resulting dataset, I have simulated a quantitative trait that is under the control of a number of SNPs. The trait is in the file qtrait.dat. There is a little bit of population heterogeneity of gene action.
Therefore, it will be worthwhile to do some preliminary analysis looking for effects of sex and population of origin
Where do we find that information?
You should be able to find a file called relationships_w_pops_051208.txt. We can merge this with qtrait.dat in Excel or R, and then look for any evidence of association of the trait with the covariates.
PLINK will allow us to carry out a quantitative trait association analysis, and also allows testing for gene by environment interaction. I've listed a few different commands we might use below. Some might be a bit slow, so we should perhaps filter the best SNPs out and only perform interaction tests on those (or --qt-means). Similarly, I would try some family based association tests on the highest scoring SNPs. Why?
plink --bfile fourpops --out validate
plink --bfile fourpops --maf 0.01 --geno 0.05 --mind 0.05 \
--hwe 1e-3 --make-bed --out fourpops_clean
plink --bfile mydata --loop-assoc populations.dat --assoc
plink --bfile fourpops_clean --pheno qtrait.dat --assoc --out fourpops_res
plink --bfile fourpops_clean --pheno qtrait.dat --gxe --covar mycov.dat
plink --bfile mydate --linear --pheno qtrait.dat --covar file.cov --interaction --test-all
plink --bfile mydate --linear --pheno qtrait.dat --within populations.dat